Untersuchung mathematischer Kurven – Mathe am UEG entdecken

Was sind Kurven?

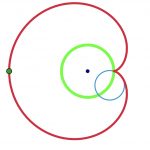
Mathematische Kurven sind ein- oder mehrdimensionale Objekte, die jeden beliebigen Verlauf annehmen und durch Funktionen oder Gleichungen beschrieben werden können. Die verschiedenen Formen, die Kurven annehmen können, zeigen die Abbildungen zweier algebraischer Kurven auf der rechten Seite.

Bei der Untersuchung werden Eigenschaften, Verhalten, Symmetrien sowie weitere spezielle Charakteristika verschiedener Arten von Kurven detailliert analysiert und erforscht. Die Untersuchung ermöglicht das Erkennen mathematischer Zusammenhänge oder das Lösen mathematischer Probleme und findet zum Beispiel Anwendung in den Ingenieurswissenschaften, der Physik oder der Wirtschaft.

Untersuchung des Flächeninhalts einer Kurve

Um einen kleinen Einblick in die Untersuchung der Kurven zu erhalten, betrachten wir am Beispiel der Lemniskate, wie man den Flächeninhalt einer Kurve bestimmen kann.

Allgemein lassen sich Flächeninhalte zwischen einem Graphen und der x-Achse mithilfe eines Integrals berechnen. Da es sich um eine Kurve handelt, die durch eine Polargleichung beschrieben werden kann, lässt sich der Flächeninhalt mit folgender Formel berechnen:

$A(\varphi_{0},\varphi_{1})=\frac{1}{2} \int_{\varphi_{0}}^{\varphi_{1}} r(\varphi)^2 d\varphi$

Dabei werden außerdem Intervallgrenzen, also bestimmte Bereiche der Funktion, die von Interesse sind, festgelegt.

Bei der Lemniskate lässt sich die Rechnung vereinfachen, indem wir nur den ersten Quadranten betrachten. Dies ist aufgrund der doppelten Achsensymmetrie möglich und das Integral kann zum Schluss einfach mit vier multipliziert werden.

Wir legen also die Intervallgrenzen 0 und $\frac{\pi}{4}$ fest und setzten die Polargleichung ein.

A=4 \cdot \frac{1}{2} \int_{0}^\frac{\pi}{4} \left(2e^2 \cos(2\varphi)\right) d(\varphi)   \\     =4e^2 \left [\frac{1}{2}\sin(2\varphi)\right ]_0^\frac{\pi}{4} \\      =2e^2

Wir erhalten den Flächeninhalt $2e^2$ der Lemniskate mit Brennpunktabstand $2e$ . Der Flächeninhalt der Lemniskate kann allerdings wie in der Abbildung zu sehen ist, auch auf anderem Wege ermittelt werden. Konstruiert man zwei Quadrate mit der Kantenlänge $e$ , die mit ihrer Diagonale genau in die Lemniskate passen, stimmt der Flächeninhalt der beiden Quadrate mit dem Flächeninhalt der Lemniskate überein.

Wenn die Untersuchung des Flächeninhalts der Lemniskate dein Interesse geweckt hat, kannst du über die Buttons zur vollständige Seminarfacharbeit oder zur Präsentation zur Facharbeit gelangen, in der neben der Lemniskate auch die Cassini‘sche Kurve analysiert wird.