Sphärische Geometrie und ihre Anwendungen in der Navigation
Die sphärische Geometrie befasst sich mit Berechnungen auf der Kugel. Da die Form unserer Erde annähernd einer Kugel entspricht, findet dieses mathematische Teilgebiet auch in der Navigation Anwendung.
Sphärische Zweiecke
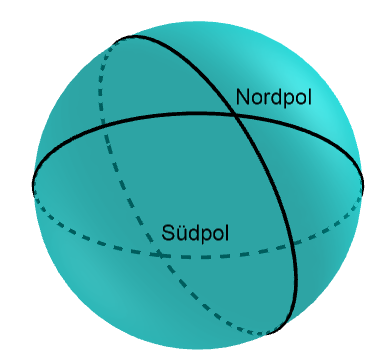
Nein, es handelt sich hier nicht um einen Tippfehler! Auf der Kugel gibt es tatsächlich Figuren mit zwei Seiten und zwei Ecken. Das liegt daran, dass in der sphärischen Geometrie andere Grundannahmen gelten als in der euklidischen. So schneiden sich zum Beispiel zwei Kugelgeraden immer in genau zwei Punkten, Parallelen gibt es nicht. Falls du dir das schwer vorstellen kannst, betrachte doch einfach das Gradnetz der Erde. Je zwei gegenüberliegende Längengrade bilden eine Kugelgerade. Alle so entstehenden Kugelgeraden verlaufen durch den Nord- und Südpol, schneiden sich also in diesen zwei Punkten. Je zwei Kugelgeraden teilen die Erdoberfläche in vier Kugelzweiecke.
Wenn dieser kleine Einblick dein Interesse geweckt hat, kannst du gerne in meine vollständige Facharbeit reinschauen. Dort werden dir neben Zweiecken weitere spannende Themen begegnen. Du erfährst zum Beispiel, was der Unterschied zwischen euklidischer und sphärischer Geometrie ist, was es mit sphärischen Dreiecken und der sphärischen Trigonometrie auf sich hat und wie man auf dieser Grundlage Kurse und Distanzen auf unserer Erde bestimmen kann.
Nein, es handelt sich hier nicht um einen Tippfehler! Auf der Kugel gibt es tatsächlich Figuren mit zwei Seiten und zwei Ecken. Das liegt daran, dass in der sphärischen Geometrie andere Grundannahmen gelten als in der euklidischen. So schneiden sich zum Beispiel zwei Kugelgeraden immer in genau zwei Punkten, Parallelen gibt es nicht. Falls du dir das schwer vorstellen kannst, betrachte doch einfach das Gradnetz der Erde. Je zwei gegenüberliegende Längengrade bilden eine Kugelgerade. Alle so entstehenden Kugelgeraden verlaufen durch den Nord- und Südpol, schneiden sich also in diesen zwei Punkten. Je zwei Kugelgeraden teilen die Erdoberfläche in vier Kugelzweiecke.
