Graphentheorie und neuronale Signalübertragung
Auf dieser Seite geht es um eine kurze Einführung in die Graphentheorie. Dabei wird deren sinnvolle Anwendung an neuronalen Netzwerken dargestellt.
- Definition eines Graphen und seine Eigenschaften
- Darstellung der Graphen in Matrizen
- Algorithmen
- Graphentheorie in Anwendung auf neuronale Netzwerke
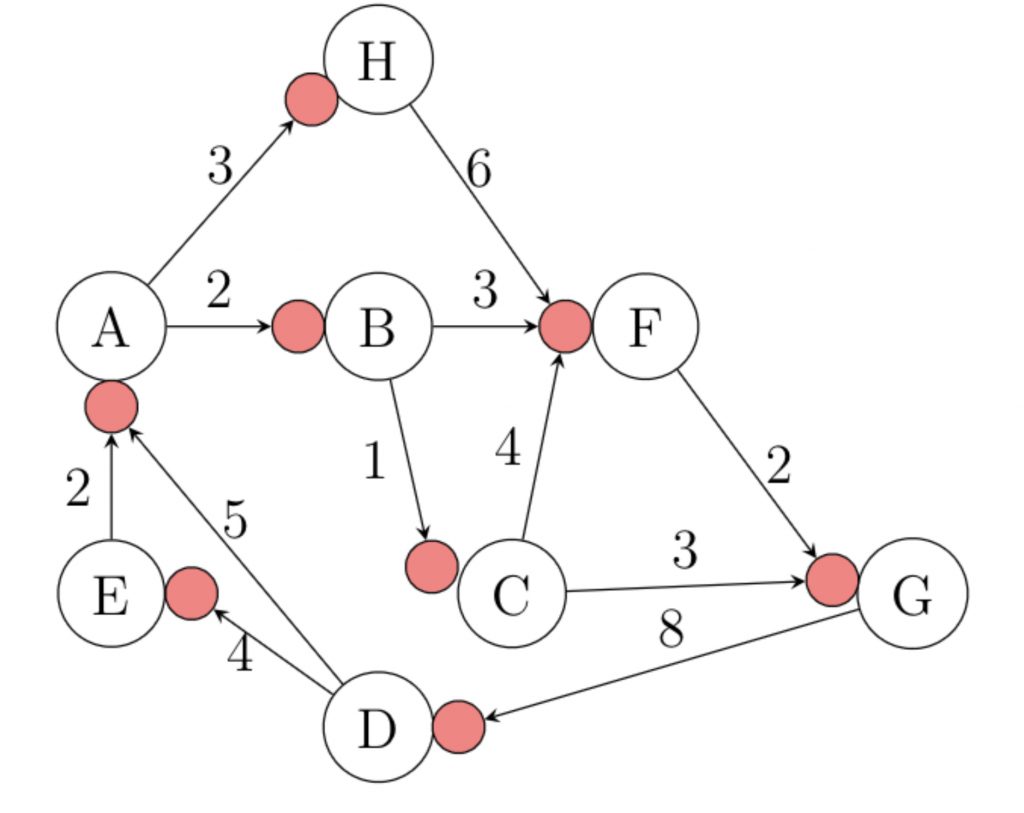
Definition eines Graphen und seine Eigenschaften
Ein Graph ist eine abstrakte Darstellung zweier oder mehr Objekte und deren Beziehung zueinander. Er hat Kanten und Ecken. Zusätzlich weist ein Graph verschiedene Eigenschaften auf (hier sind einige Beispiele gelistet):
- Gerichtet und ungerichtet
- Stark, schwach und nicht zusammenhängend
- Gewichtet und ungewichtet
- Pfade und Kreise
Darstellung der Graphen in Matrizen
Um die Beziehung zwischen Objekten anders darzustellen und bestimmte Eigenschaften genauer zu analysieren, lassen sich Graphen in Matrizen darstellen: Zwei Beispiele dafür sind die Adjazenzmatrix und die Inzidenzmatrix. Anhand der ersten Matrix kann die Benachbarung bzw. die Beziehung zwischen zwei Knoten untersucht werden (engl. adjacency: Nachbarschaft). Die Inzidenzmatrix stellt die Beziehung zwischen Knoten und Kanten dar. Durch diese Art der Darstellung kann nun bereits auf Eigenschaften des Graphen geschlossen werden.
Algorithmen
Durch Algorithmen lassen sich die Graphen genauer analysieren. Kürzeste oder günstigste Wege, sowie Wahrscheinlichkeiten werden anhand dieser berechnet. Dabei werden verschiedene Iterationen durchgeführt bis zum Abbruch des Algorithmus. Beispiele für typische Algorithmen sind die Breitensuche, die Tiefensuche, der Kruskal-Alorithmus, der Greedy-Algorithmus und der Dijkstra-Algorithmus.
Der Greedy-Algorithmus unteruscht z.B., wie der Name (engl. greedy: gierig), schon erwarten lässt, den kürzesten Weg, jedoch nur aktuell den kürzesten Weg eines Graphen. Die Erweiterung des Algorithmus ist der Dijkstra-Algorithmus. Dieser ermittelt den insgesamt kürzesten Weg innerhalb eines Graphen.
Anwendung in der Neurobiologie
In der Neurobiologie findet dieses mathematische Gebiet dann Anwendung in der Darstellung und Untersuchung des Gehirns. Durch die Kategorisierung von Netzwerken durch graphentheoretische Eigenschaften lassen sich verschiedene Bereiche des Hirns oder bei verschiedenen Abläufen untersuchen. Hierbei wird durch verschiedene bildgebende Verfahren (fmrt oder Kaliumfluoresßenz) ein Graph abstrahiert, der die Entsendung von elektrischen Impulsen eines Neuronen zu einem anderen Neuron darstellt.
Aufgrund der Darstellung und Untersuchung durch die Graphentheorie lassen sich neben der Erforschung des Gehrins (Konnektom) auch neuronale Krankheiten genauer analysieren und Therapieansätze entwickeln.
Hier finden Sie meinen Seminarfacharbeit.
Außerdem können Sie sich das Thema auch durch meine Präsentation veranschaulichen lassen.
