Wege zur Mathematisierung genetischer Verwandtschaft
Wie kann man mithilfe der Mathematik die Verwandtschaft zweier Lebewesen anhand ihrer gegebenen DNA-Sequenzen untersuchen und bestimmen, wie nah sich die Lebewesen sind? Dieser biologischen Fragestellung wurde in dieser Facharbeit nachgegangen, sodass ich anhand mathematischer Modellierung Lösungsansätze vorgestellt habe. Ziel war dabei mit der genetischen Vielfalt der gegebenen Sequenzen möglichst passende mathematische Wege zu finden. Die Bestimmung des evolutionären Abstandes basiert auf der Annahme, dass die beiden Sequenzen im Laufe der Evolution durch Mutationen aus einem gemeinsamen Vorfahren entstanden sind. Die Verwendung der Markov-Modelle ist hierbei eine Möglichkeit, die Wahrscheinlichkeit an auftretenden Mutationen zu berechnen. Ein Markov-Modell beschreibt die Veränderungen eines Systems anhand den Wahrscheinlichkeiten der einzutretenden Fälle. Auf die Biologie übertragen, ist das System die DNA-Sequenz, die sich im Laufe der Evolution durch Mutationen verändert. Hier ist die Differenzierung zwischen mehreren Mutationsarten wichtig, um der Realität näher zu kommen.
Beispiel:
Gegeben sind zwei DNA-Sequenzen
1. ATTGCTAG
2. CTTGATAG
Zuerst ermittelt man die prozentuale Abweichung p. Die Anzahl an unterschiedlichen Basen beträgt 2 von 8, d.h. 25%. Diese kann man nun in folgender Formel einsetzen:
d = −3 4 · ln(1−4/3 · 0.25) = 0.304
Der Abstand (d= distance) zwischen den beiden Sequenzen beträgt somit 0,304; es gibt also ca. 0,304 Mutation pro Stelle zwischen den beiden Sequenzen. Im nächsten Schritt muss man eine andere Methode anwenden, dass ist die Differenzierung zwischen mehreren Mutationsarten gewährleistet wird, um der Realität näher zu kommen.
Mutationsarten:
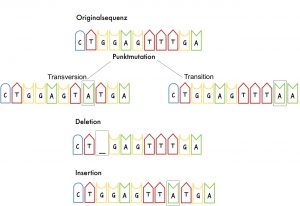
Hier finden Sie meine Seminarfacharbeit.
