Didaktik der komplexen Zahlen

Was sind komplexe Zahlen?

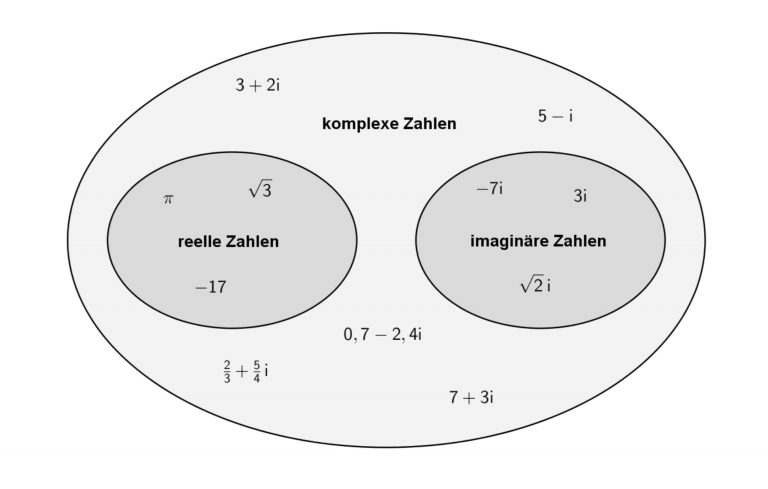
Komplexe Zahlen sind die Erweiterung des Zahlbereichs, der auf die Erweiterung durch die reellen Zahlen folgt. Im Gegensatz zu den reellen Zahlen werden diese aus verschiedenen Elementen zusammengesetzt. Hierbei gibt es den  Realteil und den Imaginärteil. Der Realteil besteht aus einer reellen Zahl und der Imaginärteil aus i und b wobei b eine reelle Zahl ist. Eine komplexe Zahl z ist dann wie folgt zusammengesetzt z=a+bi .

Wie werden komplexe Zahlen unterrichtet?

Um komplexe Zahlen im Unterricht der gymnasialen Oberstufe zu behandeln, gibt es verschiedene Vorgehensweisen. Hierbei können beispielsweise auch Bezüge zur Vektorgeometrie hergestellt werden.

Auf dem Zahlenstrahl der reellen Zahlen könne diese als Vektor dargestellt werden wobei die Zahlen selbst den Vektor darstellen. Dieses Konzept ist auch auf komplexe Zahlen anwendbar wenn man sie auf einer Zahlenebene projeziert. Hierbei gibt der Realteil die Verschiebung nach links und rechts an und der Imaginärteil die Verschiebung nach oben und unten. Genau wie normale Vektoren können auch diese Addiert und Subtrahiert werden.

Bei der Darstellung in der Polarform werden Zahlen durch ein Argument 𝜑 und den Betrag |z| angegeben. |z|*E(𝜑)

Verschiedene Darstellungsformen: Polarform, Zahlenebene